Dithering
Table of Contents
Dithering works by approximating unavailable colors with available colors, by mixing and matching available colors in a way that mimicks unavailable ones.
The basic idea behind dithering is error diffusion.
If you start with quantizing colors to either 0 or 255, then consider an image that looks like the following:
|---+----+-----| | 0 | 96 | 255 | |---+----+-----|
Since 96 is closer to 0, we will quantize to black. If we have a bunch of 96 valued pixels, then we’ll have all black pixels and no representation of gray pixels. Error diffusion works by “diffusing” the error out to neighboring pixels.
A simple example: When a pixel with value 96 is found, it assigns value of 0, but notes that we have accumulated an error of 96 away from it’s true value. If the next pixel is again 96, we add the previous error, totaling 192. 192 is closer to white, so this pixel gets 255 and the new accumulated error 192 - 255 = -63. In this manner the algorithm can continue alternating between black and white pixels to account for the gray pixels it encounters.
A similar picture works in 2D as well.
All standard image dithering algorithms push error forward, never backwards.
Clever dithering algorithms will follow a serpentine path, where left-to-right directionality is reversed each line. This can reduce spots of uniform speckling and give a more varied appearance, but it’s more complicated to implement.
1. Floyd-Steinberg
The error diffusion stencil looks like this:
|------+------+------| | 0 | X | 7/16 | |------+------+------| | 3/16 | 5/16 | 1/16 | |------+------+------|
where, X is the current pixel. Same as our example, if current pixel is 96 and
is to be quantized down to 0, the error is 96, which is distributed relatve to
the proportions listed in the stencil. The errors will be:
|----+----+----| | 0 | X | 42 | |----+----+----| | 18 | 30 | 6 | |----+----+----|
This is well known and fairly efficient to implement. Additionally, since divisor is 16, it can be computed with a few bit-shifts making it fast even on older hardware.
2. Jarvis-Judice-Ninke
|---+---+---+---+---| | 0 | 0 | X | 7 | 5 | | 3 | 5 | 7 | 5 | 3 | * 1/48 | 1 | 3 | 5 | 3 | 1 | |---+---+---+---+---|
With this algorithm, the error is distributed to three times as many pixels as in Floyd-Steinberg, leading to much smoother – and more subtle – output.
Another downside of the JJN filter is that it pushes the error down not just one row, but two rows. This means we have to keep two forward arrays – one for the next row, and another for the row after that.
3. Stucki
|---+---+---+---+---| | 0 | 0 | X | 8 | 4 | | 2 | 4 | 8 | 4 | 2 | * 1/42 | 1 | 2 | 4 | 2 | 1 | |---+---+---+---+---|
For most images, there will be minimal difference between the output of Stucki and JJN algorithms.
4. Atkinson
Developed by Bill Atkinson while at Apple working on MacPaint. Bill Atkinson is also know for inventing the Marching ants you often see in many image selection programs. His muse for the marching ants is also quite amusing.
Atkinson’s formula is a bit different from others in this list, because it only propagates a fraction of the error instead of the full amount. This technique is sometimes offered by modern graphics applications as a “reduced color bleed” option. By only propagating part of the error, speckling is reduced, but contiguous dark or bright sections of an image may become washed out.
|---+---+---+---| | 0 | X | 1 | 1 | | 1 | 1 | 1 | 0 | * 1/8 | 0 | 1 | 0 | 0 | |---+---+---+---|
5. Burkes
|---+---+---+---+---| | 0 | 0 | X | 8 | 4 | * 1/32 | 2 | 4 | 8 | 4 | 2 | |---+---+---+---+---|
Similar to Stucki but with power of 2 divisor.
6. Sierra
|---+---+---+---+---| | 0 | 0 | X | 5 | 3 | | 2 | 4 | 5 | 4 | 2 | * 1/32 | 0 | 2 | 3 | 2 | 0 | |---+---+---+---+---|
7. Sierra two row
|---+---+---+---+---| | 0 | 0 | X | 4 | 3 | * 1/16 | 1 | 2 | 3 | 2 | 1 | |---+---+---+---+---|
8. Sierra lite
+---+---+---+ | 0 | X | 2 | * 1/4 | 1 | 1 | 0 | |---+---+---+
9. Void and cluster
Have the advantage of ordered dithering in that they are highly parallelization, e.g. via GPU shaders but do not leave the easily spottable patterns of ordered dithering. Two papers below describe the void and cluster algorithm:
- void and cluster method by Robert Ulichney
- Spatial Extent of Void and Cluster Finding Filters by Robert Ulichney
madVR video renderer uses it for realtime video dithering to avoid banding shallow color gradients from 10bit sources or debanded internal 16bit representation on <= 8bit displays.
10. Uses
Dithering is not only used for limited color spaces. Generalizing further, if you have high or infinite precision in your color values, dithering will look much nicer than simply rounding to the nearest value. A concrete example is a color gradient. If done naively with rounding, color bands will be clearly visible. With dithering, they will be almost impossible to see. See this experiment by Johannes Hoff
11. Image parsing directions
While image parsing order does not matter with ordered dithering, it can actually be crucial with error diffusion. The reason is that once a pixel has been processed, standard error diffusion methods do not go back.
Typical raster dithering:
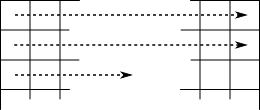
Figure 1: raster image dithering order
Serpentine ordering:
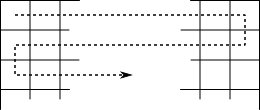
Figure 2: serpentine parsing
We can also use hilbert curves. However, an inherent problem with plane-filling curves is that distances on the curve do not mean anything in image space. Generally these don’t produce decent results for error diffusion in images at least. Error diffusion for audio signals perhaps?
12. Temporal dithering
The following are notes courtesy of Don Hopkins:
Iteratively diffusing errors can not only be used for unvisited neighbors to the right and down but also into the future.
It works nicely with video, and it makes still images (and images you’re slowly panning and zooming with the Ken Burns effect) look alive and detailed, as if they were live video.
Another variation of the serpentine scanning (the boustrophedon transform) you can apply when iteratively dithering an image is to rotate the scan direction 90 degrees each frame, so even frames scan horizontally, odd frames scan vertically, and the vertical and horizontal scan directions rotate round every four frames. That results in a completely uniform diffusion, even when each scan frame only diffuses errors to the next cell.
It spreads the error out over time, as well as space, which has a pleasing effect on the eyes, I think. Any one frame has artifacts, but they tend to cancel each other out over time, break up the log jams, and dance around local minima and without getting stuck at fixed points.
13. Art and stylization
The coolest use of dithering I have seen is from the game The Return of Obra Dinn by Lucas Pope. He created a variant of a dithering algorithm to make faces look better for the game. Check it out here.
A copy of the shader by Lucas Pope can be found on github here. Otherwise, I have a cached copy DitherShader
14. Further reading
- Checkout the science behind colour ASCII art.
- Some more dithering procedures.